Introduction

1. Texas Holdem Hand Odds Probabilities Calculator
2. Texas Holdem Hand Odds Probabilities Probability

In Texas Hold 'Em a hand is said to be dominated if another player has a similar, and better, hand. To be more specific, a dominated hand is said to rely on three or fewer outs (cards) to beat the hand dominating it, not counting difficult multiple-card draws. There are four types of domination, as follows.

1. A pair is dominated by a higher pair. For example J-J is dominated by Q-Q. Only two cards help the J-J, the other two jacks.
2. A non-pair is dominated by a pair of either card. For example, Q-5 is dominated by Q-Q or 5-5. In the case of 5-5, three cards only will help the Q-5, the other three queens.
3. A non-pair is dominated by a pair greater than the lower card. For example, Q-5 is dominated by 8-8. Only three cards will help the Q-5, the other three queens.
4. A non-pair is dominated by another non-pair if there if there is a shared card, and the rank of the opponent's non-shared card is greater the dominated non-shared card. For example Q-5 is dominated by K-5 or Q-7. In the former case (K-5 over Q-5) only three cards can help Q-5, the other three queens.

That said, the following tables present the probability of every two-card hand being dominated, according to the total number of players.

Texas Hold'em Poker probabilities When calculating probabilities for a card game such as Texas Hold'em, there are two basic approaches. The first approach is to determine the number of outcomes that satisfy the condition being evaluated and divide this by the total number of possible outcomes. When you understand odd calculation and probability you will be able to determine your odds of winning in any Texas Holdem situation and, based on these odds, you will be able to make the best betting decision. To determine your pot odds you need to figure out the ratio of the total pot that you are contributing in each hand. The cumulative probability is determined by adding one hand's probability with the probabilities of all hands above it. The Odds are defined as the ratio of the number of ways not to draw the hand, to the number of ways to draw it. In statistics, this is called odds against. For instance, with a royal flush, there are 4 ways to draw one,.

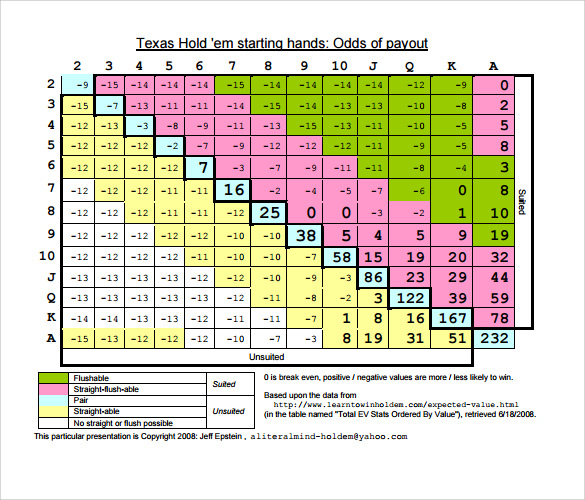
Probability of Domination — PairsExpand

Cards	2 Players	3 Players	4 Players	5 Players	6 Players	7 Players	8 Players	9 Players	10 Players
2,2	0.0588	0.1142	0.1659	0.2150	0.2609	0.3044	0.3449	0.3835	0.4195
3,3	0.0540	0.1049	0.1532	0.1983	0.2419	0.2826	0.3212	0.3576	0.3922
4,4	0.0489	0.0956	0.1400	0.1820	0.2220	0.2602	0.2966	0.3313	0.3640
5,5	0.0441	0.0862	0.1265	0.1653	0.2021	0.2376	0.2710	0.3031	0.3345
6,6	0.0392	0.0767	0.1133	0.1481	0.1816	0.2136	0.2448	0.2745	0.3036
7,7	0.0344	0.0675	0.0996	0.1306	0.1605	0.1895	0.2177	0.2447	0.2709
8,8	0.0295	0.0581	0.0858	0.1129	0.1391	0.1648	0.1894	0.2138	0.2369
9,9	0.0246	0.0485	0.0720	0.0947	0.1173	0.1391	0.1604	0.1813	0.2017
T,T	0.0196	0.0389	0.0578	0.0765	0.0947	0.1126	0.1300	0.1478	0.1649
J,J	0.0147	0.0293	0.0435	0.0577	0.0719	0.0856	0.0992	0.1132	0.1262
Q,Q	0.0098	0.0195	0.0292	0.0389	0.0483	0.0579	0.0674	0.0766	0.0861
K,K	0.0049	0.0098	0.0147	0.0196	0.0245	0.0294	0.0341	0.0391	0.0439
A,A	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000	0.0000

Texas Holdem Hand Odds Probabilities Calculator

Probability of Domination — Non-PairsExpand

Cards	2 Players	3 Players	4 Players	5 Players	6 Players	7 Players	8 Players	9 Players	10 Players
3,2	0.2742	0.4785	0.6289	0.7389	0.8187	0.8753	0.9156	0.9438	0.9629
4,2	0.2645	0.4634	0.6124	0.7227	0.8036	0.8626	0.9049	0.9350	0.9562
4,3	0.2496	0.4417	0.5877	0.6986	0.7815	0.8433	0.8888	0.9220	0.9459
5,2	0.2546	0.4487	0.5956	0.7060	0.7881	0.8489	0.8934	0.9255	0.9486
5,3	0.2399	0.4263	0.5701	0.6805	0.7645	0.8279	0.8754	0.9108	0.9367
5,4	0.2253	0.4036	0.5439	0.6539	0.7393	0.8050	0.8556	0.8937	0.9227
6,2	0.2450	0.4338	0.5786	0.6885	0.7718	0.8344	0.8809	0.9152	0.9403
6,3	0.2302	0.4110	0.5525	0.6620	0.7470	0.8118	0.8614	0.8986	0.9266
6,4	0.2154	0.3881	0.5254	0.6344	0.7199	0.7869	0.8394	0.8796	0.9105
6,5	0.2008	0.3647	0.4975	0.6047	0.6911	0.7599	0.8146	0.8581	0.8919
7,2	0.2350	0.4186	0.5611	0.6709	0.7550	0.8191	0.8676	0.9042	0.9311
7,3	0.2204	0.3955	0.5340	0.6430	0.7285	0.7948	0.8461	0.8854	0.9155
7,4	0.2057	0.3724	0.5065	0.6138	0.7000	0.7681	0.8220	0.8642	0.8971
7,5	0.1910	0.3484	0.4776	0.5833	0.6693	0.7388	0.7951	0.8402	0.8761
7,6	0.1763	0.3244	0.4478	0.5510	0.6365	0.7071	0.7651	0.8128	0.8514
8,2	0.2255	0.4034	0.5434	0.6526	0.7375	0.8032	0.8536	0.8923	0.9213
8,3	0.2105	0.3800	0.5157	0.6237	0.7095	0.7771	0.8300	0.8714	0.9034
8,4	0.1959	0.3563	0.4870	0.5932	0.6791	0.7481	0.8037	0.8478	0.8828
8,5	0.1812	0.3323	0.4574	0.5614	0.6467	0.7168	0.7743	0.8208	0.8586
8,6	0.1666	0.3078	0.4272	0.5277	0.6122	0.6829	0.7416	0.7904	0.8311
8,7	0.1518	0.2829	0.3952	0.4922	0.5750	0.6453	0.7056	0.7563	0.7992
9,2	0.2156	0.3878	0.5250	0.6338	0.7194	0.7862	0.8388	0.8793	0.9104
9,3	0.2010	0.3643	0.4968	0.6039	0.6895	0.7583	0.8130	0.8564	0.8904
9,4	0.1862	0.3402	0.4674	0.5720	0.6577	0.7274	0.7843	0.8300	0.8668
9,5	0.1714	0.3157	0.4371	0.5388	0.6234	0.6937	0.7523	0.8003	0.8398
9,6	0.1569	0.2911	0.4061	0.5036	0.5868	0.6573	0.7167	0.7667	0.8088
9,7	0.1419	0.2658	0.3734	0.4669	0.5476	0.6174	0.6776	0.7289	0.7730
9,8	0.1274	0.2403	0.3400	0.4282	0.5061	0.5742	0.6342	0.6867	0.7320
T,2	0.2057	0.3722	0.5066	0.6143	0.7005	0.7688	0.8229	0.8654	0.8987
T,3	0.1910	0.3485	0.4772	0.5831	0.6691	0.7387	0.7950	0.8402	0.8762
T,4	0.1764	0.3240	0.4474	0.5501	0.6352	0.7055	0.7638	0.8111	0.8499
T,5	0.1617	0.2995	0.4163	0.5153	0.5991	0.6696	0.7286	0.7784	0.8196
T,6	0.1470	0.2742	0.3843	0.4790	0.5606	0.6305	0.6904	0.7413	0.7847
T,7	0.1323	0.2487	0.3512	0.4411	0.5196	0.5881	0.6478	0.6996	0.7448
T,8	0.1176	0.2227	0.3169	0.4008	0.4754	0.5418	0.6009	0.6532	0.6993
T,9	0.1030	0.1965	0.2817	0.3586	0.4286	0.4923	0.5492	0.6010	0.6473
J,2	0.1960	0.3566	0.4877	0.5944	0.6808	0.7505	0.8063	0.8508	0.8862
J,3	0.1813	0.3324	0.4578	0.5617	0.6476	0.7180	0.7757	0.8227	0.8610
J,4	0.1665	0.3078	0.4271	0.5275	0.6120	0.6828	0.7419	0.7911	0.8317
J,5	0.1519	0.2827	0.3954	0.4916	0.5741	0.6441	0.7042	0.7549	0.7976
J,6	0.1371	0.2573	0.3621	0.4537	0.5336	0.6026	0.6625	0.7143	0.7590
J,7	0.1223	0.2314	0.3284	0.4142	0.4901	0.5572	0.6164	0.6688	0.7145
J,8	0.1077	0.2050	0.2931	0.3725	0.4442	0.5083	0.5658	0.6174	0.6638
J,9	0.0931	0.1785	0.2571	0.3289	0.3948	0.4553	0.5100	0.5601	0.6061
J,T	0.0783	0.1515	0.2199	0.2837	0.3427	0.3979	0.4493	0.4967	0.5409
Q,2	0.1862	0.3406	0.4685	0.5739	0.6604	0.7312	0.7886	0.8352	0.8727
Q,3	0.1713	0.3161	0.4379	0.5402	0.6255	0.6968	0.7557	0.8044	0.8445
Q,4	0.1568	0.2910	0.4062	0.5045	0.5880	0.6590	0.7189	0.7696	0.8119
Q,5	0.1422	0.2658	0.3736	0.4671	0.5482	0.6180	0.6783	0.7299	0.7744
Q,6	0.1273	0.2400	0.3400	0.4280	0.5055	0.5734	0.6333	0.6857	0.7312
Q,7	0.1126	0.2139	0.3048	0.3868	0.4600	0.5254	0.5835	0.6357	0.6818
Q,8	0.0979	0.1875	0.2691	0.3435	0.4113	0.4730	0.5289	0.5800	0.6257
Q,9	0.0833	0.1606	0.2321	0.2983	0.3600	0.4166	0.4689	0.5173	0.5619
Q,T	0.0687	0.1332	0.1940	0.2516	0.3052	0.3557	0.4032	0.4480	0.4894
Q,J	0.0540	0.1055	0.1547	0.2020	0.2474	0.2902	0.3313	0.3707	0.4082
K,2	0.1763	0.3246	0.4491	0.5532	0.6395	0.7111	0.7702	0.8185	0.8579
K,3	0.1616	0.2998	0.4178	0.5178	0.6027	0.6740	0.7343	0.7848	0.8269
K,4	0.1469	0.2745	0.3851	0.4808	0.5633	0.6343	0.6948	0.7466	0.7908
K,5	0.1322	0.2491	0.3517	0.4422	0.5211	0.5904	0.6509	0.7037	0.7494
K,6	0.1175	0.2230	0.3171	0.4013	0.4763	0.5431	0.6025	0.6550	0.7016
K,7	0.1029	0.1964	0.2814	0.3586	0.4285	0.4918	0.5490	0.6007	0.6473
K,8	0.0881	0.1697	0.2447	0.3139	0.3777	0.4367	0.4905	0.5397	0.5853
K,9	0.0734	0.1423	0.2069	0.2675	0.3238	0.3765	0.4259	0.4720	0.5148
K,T	0.0588	0.1146	0.1678	0.2183	0.2665	0.3120	0.3555	0.3961	0.4350
K,J	0.0441	0.0866	0.1277	0.1671	0.2058	0.2426	0.2780	0.3125	0.3452
K,Q	0.0294	0.0582	0.0865	0.1141	0.1414	0.1679	0.1940	0.2195	0.2444
A,2	0.1665	0.3086	0.4294	0.5316	0.6177	0.6901	0.7505	0.8009	0.8425
A,3	0.1517	0.2835	0.3970	0.4949	0.5791	0.6509	0.7120	0.7641	0.8080
A,4	0.1372	0.2578	0.3636	0.4565	0.5376	0.6082	0.6695	0.7227	0.7684
A,5	0.1224	0.2318	0.3294	0.4164	0.4934	0.5618	0.6223	0.6754	0.7225
A,6	0.1077	0.2054	0.2940	0.3741	0.4462	0.5115	0.5702	0.6228	0.6701
A,7	0.0931	0.1787	0.2575	0.3300	0.3963	0.4572	0.5129	0.5638	0.6101
A,8	0.0783	0.1516	0.2200	0.2837	0.3428	0.3983	0.4498	0.4976	0.5418
A,9	0.0637	0.1241	0.1810	0.2352	0.2866	0.3347	0.3804	0.4237	0.4647
A,T	0.0490	0.0959	0.1411	0.1847	0.2264	0.2664	0.3049	0.3417	0.3770
A,J	0.0343	0.0677	0.1003	0.1320	0.1629	0.1931	0.2223	0.2507	0.2784
A,Q	0.0195	0.0389	0.0582	0.0769	0.0956	0.1140	0.1320	0.1500	0.1676
A,K	0.0049	0.0098	0.0147	0.0195	0.0243	0.0292	0.0340	0.0388	0.0436

Methodology: These tables were created by a random simulation. Each cell in the table above for pairs was based on 7.8 million hands, and 21.7 million for the non-pairs.

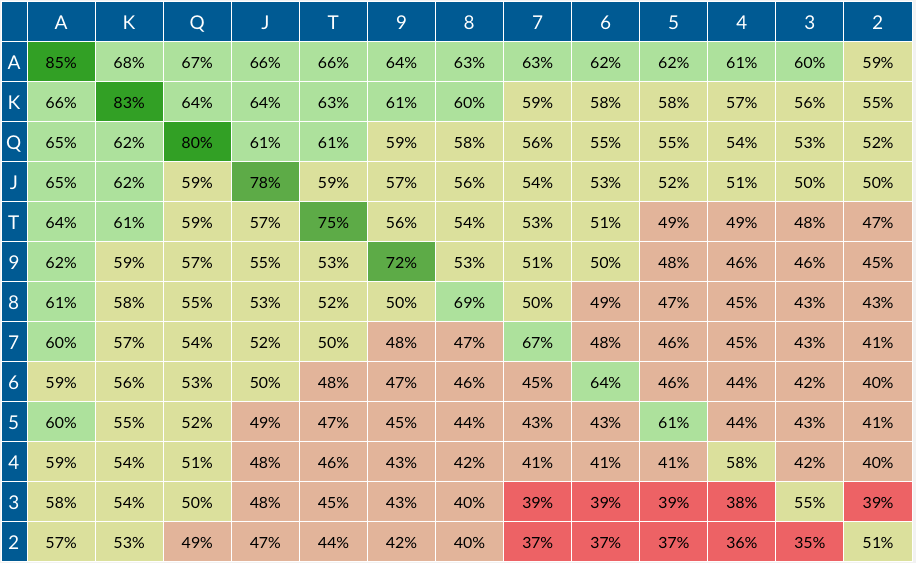
2-Player Formula

The probability of domination in a two player game is easy to calculate. For pairs it is 6×(number of higher ranks)/1225. For example, the probability a pair of eights is dominated is 6×6/1225 = 0.0294, because there are six ranks higher than 8 (9,T,J,Q,K,A).

Texas Holdem Hand Odds Probabilities Probability

For non-pairs the formula is (6+18×(L-1)+12×H)/1225, where

L=Number of ranks higher than lower card
H=Number of ranks higher than higher card

For example, the probability that J-7 is dominated is (6+18×(7-1)+12×3)/1225 = 150/1225 = 0.1224.

Written by: Michael Shackleford